Çözüldü Trigonometri Soruları
- Konuyu başlatan Frastoly
- Başlangıç Tarihi
- Mesaj 3
- Görüntüleme 3.579
-
- Etiketler
- matematik trigonometri
Bu konu çözüldü olarak işaretlenmiştir. Çözülmediğini düşünüyorsanız konuyu rapor edebilirsiniz.
Çözüm
İlk soruda açı yüzünden sin pozitiftir, aynı çıkar.
Cos negatiftir, -cosx olarak çıkar.
Tan negatiftir, -tanx olarak çıkar.
Cosx de cosx zaten.
Tan = sin/cos olduğu için -tanx*cosx = -sinx olur. Yani ifademiz sinx -cosx - sinx olur. Sinx'ler birbirini götürür ve -cosx kalır.
Birim çemberi bilmek yeterli.
İkinci soruda açı verilmiş. tan(-70') (derece için kullanıyorum) -tan(70')'ye eşittir. cot(70') de 1/tan(70') oluyor. Yani -tan(70') yerine -1/x yazıyoruz.
cot(-200') için karışık geldi diye 360 ekleyip 160 yapıyorum. cot (90'+70') şeklinde yazabiliyoruz. 90 olduğu için isim değiştirir, tan olur. bölgesi yüzünden negatif olur. Yani -tan(70')'ye eşittir. Bunun -1/x olduğunu söylemiştik. Pay kısmı -2/x oldu.
Paydada tan(20') ile cot(70') eşit olduğu için x oluyor.
Yine 360 ekleyelim ve 110' olsun. cot(180-70) şeklinde yazınca aynı kalır, negatif olur. Ama bir de başında da negatif var, oradan pozitif olur. Yani bu da x.
Payımız -2/x, paydamız da 2x oldu. Bölünce A şıkkı geliyor.
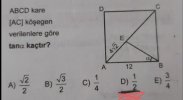
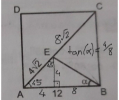
Üçüncüde E'den dik indirip K diyelim. EAB 45 derece, çünkü kare. Bu yüzden EK ve AK 4 olur. KB de 8 olduğu için tan(a) 1/2.
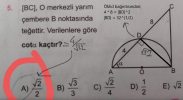
Dördüncü soruda AB çap olduğu için ABC dik. B'den D'ye dik indirebiliyoruz çünkü D çapı görüyor. Öklid ile BD kök32. ADB dik üçgenin hazır. 4/kök32'den cevap A.
Cos negatiftir, -cosx olarak çıkar.
Tan negatiftir, -tanx olarak çıkar.
Cosx de cosx zaten.
Tan = sin/cos olduğu için -tanx*cosx = -sinx olur. Yani ifademiz sinx -cosx - sinx olur. Sinx'ler birbirini götürür ve -cosx kalır.
Birim çemberi bilmek yeterli.
İkinci soruda açı verilmiş. tan(-70') (derece için kullanıyorum) -tan(70')'ye eşittir. cot(70') de 1/tan(70') oluyor. Yani -tan(70') yerine -1/x yazıyoruz.
cot(-200') için karışık geldi diye 360 ekleyip 160 yapıyorum. cot (90'+70') şeklinde yazabiliyoruz. 90 olduğu için isim değiştirir, tan olur. bölgesi yüzünden negatif olur. Yani -tan(70')'ye eşittir. Bunun -1/x olduğunu söylemiştik. Pay kısmı -2/x oldu.
Paydada tan(20') ile cot(70') eşit olduğu için x oluyor.
Yine 360 ekleyelim ve 110' olsun. cot(180-70) şeklinde yazınca aynı kalır, negatif olur. Ama bir de başında da negatif var, oradan pozitif olur. Yani bu da x.
Payımız -2/x, paydamız da 2x oldu. Bölünce A şıkkı geliyor.
Üçüncüde E'den dik indirip K diyelim. EAB 45 derece, çünkü kare. Bu yüzden EK ve AK 4 olur. KB de 8 olduğu için tan(a) 1/2.
Dördüncü soruda AB çap olduğu için ABC dik. B'den D'ye dik indirebiliyoruz çünkü D çapı görüyor. Öklid ile BD kök32. ADB dik üçgenin hazır. 4/kök32'den cevap A.
İlk soruda açı yüzünden sin pozitiftir, aynı çıkar.
Cos negatiftir, -cosx olarak çıkar.
Tan negatiftir, -tanx olarak çıkar.
Cosx de cosx zaten.
Tan = sin/cos olduğu için -tanx*cosx = -sinx olur. Yani ifademiz sinx -cosx - sinx olur. Sinx'ler birbirini götürür ve -cosx kalır.
Birim çemberi bilmek yeterli.
İkinci soruda açı verilmiş. tan(-70') (derece için kullanıyorum) -tan(70')'ye eşittir. cot(70') de 1/tan(70') oluyor. Yani -tan(70') yerine -1/x yazıyoruz.
cot(-200') için karışık geldi diye 360 ekleyip 160 yapıyorum. cot (90'+70') şeklinde yazabiliyoruz. 90 olduğu için isim değiştirir, tan olur. bölgesi yüzünden negatif olur. Yani -tan(70')'ye eşittir. Bunun -1/x olduğunu söylemiştik. Pay kısmı -2/x oldu.
Paydada tan(20') ile cot(70') eşit olduğu için x oluyor.
Yine 360 ekleyelim ve 110' olsun. cot(180-70) şeklinde yazınca aynı kalır, negatif olur. Ama bir de başında da negatif var, oradan pozitif olur. Yani bu da x.
Payımız -2/x, paydamız da 2x oldu. Bölünce A şıkkı geliyor.
Üçüncüde E'den dik indirip K diyelim. EAB 45 derece, çünkü kare. Bu yüzden EK ve AK 4 olur. KB de 8 olduğu için tan(a) 1/2.
Dördüncü soruda AB çap olduğu için ABC dik. B'den D'ye dik indirebiliyoruz çünkü D çapı görüyor. Öklid ile BD kök32. ADB dik üçgenin hazır. 4/kök32'den cevap A.
Cos negatiftir, -cosx olarak çıkar.
Tan negatiftir, -tanx olarak çıkar.
Cosx de cosx zaten.
Tan = sin/cos olduğu için -tanx*cosx = -sinx olur. Yani ifademiz sinx -cosx - sinx olur. Sinx'ler birbirini götürür ve -cosx kalır.
Birim çemberi bilmek yeterli.
İkinci soruda açı verilmiş. tan(-70') (derece için kullanıyorum) -tan(70')'ye eşittir. cot(70') de 1/tan(70') oluyor. Yani -tan(70') yerine -1/x yazıyoruz.
cot(-200') için karışık geldi diye 360 ekleyip 160 yapıyorum. cot (90'+70') şeklinde yazabiliyoruz. 90 olduğu için isim değiştirir, tan olur. bölgesi yüzünden negatif olur. Yani -tan(70')'ye eşittir. Bunun -1/x olduğunu söylemiştik. Pay kısmı -2/x oldu.
Paydada tan(20') ile cot(70') eşit olduğu için x oluyor.
Yine 360 ekleyelim ve 110' olsun. cot(180-70) şeklinde yazınca aynı kalır, negatif olur. Ama bir de başında da negatif var, oradan pozitif olur. Yani bu da x.
Payımız -2/x, paydamız da 2x oldu. Bölünce A şıkkı geliyor.
Üçüncüde E'den dik indirip K diyelim. EAB 45 derece, çünkü kare. Bu yüzden EK ve AK 4 olur. KB de 8 olduğu için tan(a) 1/2.
Dördüncü soruda AB çap olduğu için ABC dik. B'den D'ye dik indirebiliyoruz çünkü D çapı görüyor. Öklid ile BD kök32. ADB dik üçgenin hazır. 4/kök32'den cevap A.
Son düzenleme:
- Katılım
- 3 Ağustos 2020
- Mesajlar
- 2.158
- Makaleler
- 1
- Çözümler
- 26
